Geometria: problemi svolti sui triangoli
Sui lati di un triangolo equilatero ABC si prendono i punti rispettivamente D, E e F in modo tale che AD ≅ BE ≅ CF.
Dimostrare che il triangolo DEF è anch’esso equilatero.
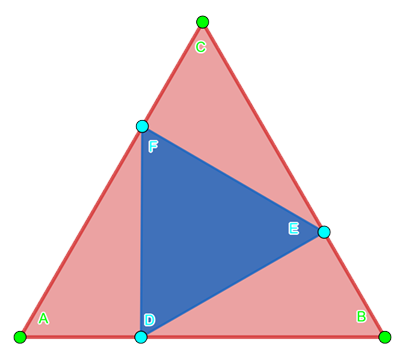
Per ipotesi si ha che gli angoli e i lati del triangolo ABC sono congruenti così come sono congruenti i segmenti AD, BE e CF.
Di conseguenza sono congruenti anche BD, CE e AF in quanto ognuno differenza di segmenti congruenti.
Per il Primo Criterio di Congruenza, allora, i tre triangoli ADF, BDE e CEF sono congruenti e quindi saranno congruenti anche i lati del triangolo DEF.
Il triangolo DEF è allora equilatero.
Visite: 23646
mercoledì 2 Giugno - 2021
