Matematica: le equazioni di secondo grado con esempi svolti
Una equazione può essere definita come una uguaglianza fra due espressioni algebriche, in cui compaiono una o più variabili, dette incognite; essa risulta verificata soltanto per particolari valori, chiamati radici o soluzioni, assunti dalle incognite che in essa figurano.
Una equazione algebrica di secondo grado (detta anche quadratica) è un’equazione algebrica con una sola incognita avente grado massimo pari a 2; la sua forma normale o canonica è del tipo:
$$\displaystyle{ax^2+bx+c=0} \;\;\;\;(a\neq0)$$
Se tutti i coefficienti sono diversi da zero l’equazione prende il nome di quadratica completa;
Se \(c=0\) l’equazione si chiama spuria e la forma diventa \(\displaystyle{ax^2+bx=0}\);
Se \(b=0\) l’equazione si chiama pura e la forma diventa \(\displaystyle{ax^2+c=0}\);
Se \(b=0\) e \(c=0\) l’equazione si chiama monomia e la forma diventa \(\displaystyle{ax^2=0}\).
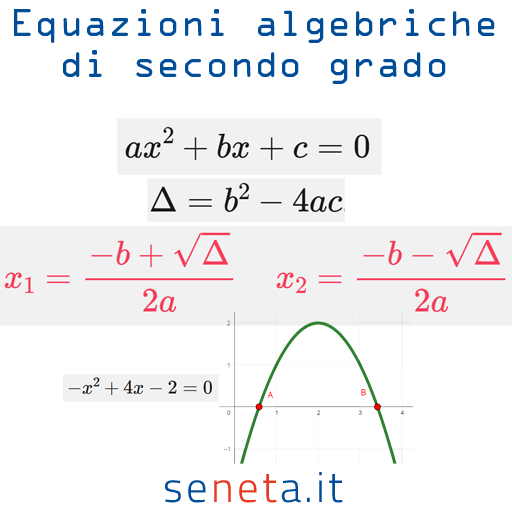
Calcolo delle soluzioni
Esercizi
– \(2x^2+7x+3=0\)
– \(x^2-14x+24=0\)
– \(2x^2-3x+20=0\)
– \(4x^2-4x+1=0\)
– \(3x^2+4x-4=0\)
– \(-x^2+2x=0\)
– \(x^2-25=0\)
Visite: 2215
