Fisica – I moti nel piano: il moto dei proiettili con esercizi
I moti del piano
Un moto piano può essere descritto attraverso il classico sistema di riferimento cartesiano per quanto riguarda la traiettoria e un cronometro per la misura del tempo; la posizione di un punto P è individuata da un’ascissa e un’ordinata.
In alternativa, per specificare un punto P del piano è possibile utilizzare il vettore posizione, che congiunge l’origine O degli assi cartesiano con il punto in questione.
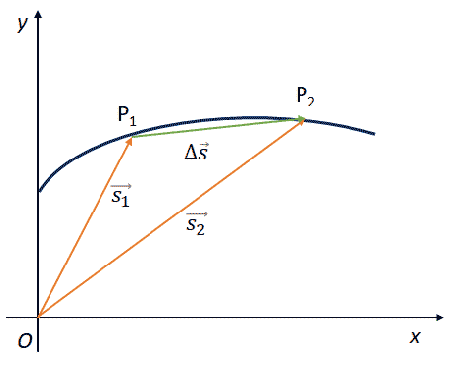
Chiamiamo vettore posizione \( \vec s\) di un punto P rispetto all’origine O degli assi coordinati il vettore che ha la coda in O e la punta in P; di conseguenza lo spostamento compiuto da un punto materiale in movimento è il vettore che ha l’origine nella posizione di partenza \(P_1\) e la punta nella posizione di arrivo \(P_2\).
Il vettore spostamento \(\vec {\Delta s}\): quindi, come rappresentato nella figura precedente, se \(\vec s_1\) rappresenta la posizione di un punto materiale a un istante \(t_1\) e \(\vec s_2\) la sua posizione all’istante \(t_2\), allora il suo spostamento \(\vec {\Delta s}\) nell’intervallo \(\Delta t = t_2 -t_1\) non è altro che la la differenza tra \(\vec{s_2}\) e \(\vec{s_1}\).
Come è possibile notare, lo spostamento \(\vec {\Delta s}\) mostra il risultato complessivo del moto, ma non fornisce né informazioni sulla traiettoria né sulla lunghezza del cammino percorso.
Per logica, come lo spostamento, nei moti piani sia la velocità che l’accelerazione sono rappresentate da vettori.
In particolare. la velocità vettoriale media \(\vec {v_m}\) assuma sempre ha sempre la stessa direzione e lo stesso verso dello spostamento \(\vec {\Delta s}\); il vettore accelerazione è il rapporto tra la variazione \(\vec {\Delta v}\) della velocità vettoriale istantanea e l’intervallo di tempo \(\Delta t\) in cui avviene tale variazione.
Visite: 8177
