Matematica: le disequazioni di II grado fratte con esercizi svolti
Risolvere la seguente disequazione:
$$\displaystyle\frac{2x}{2x+2}+\displaystyle\frac{3x-2}{x^2+2x+1}+\displaystyle\frac{2-x}{(x+1)^2}+\displaystyle\frac{1}{x+1}<0$$
$$\displaystyle\frac{x}{x+1}+\displaystyle\frac{3x-2}{(x+1)^2}+\displaystyle\frac{2-x}{(x+1)^2}+\displaystyle\frac{1}{x+1}<0$$
$$\displaystyle\frac{x(x+1)+(3x-2)+(2-x)+1}{(x+1)^2}<0$$
$$\displaystyle\frac{x^2+4x+1}{(x+1)^2}<0$$
Per quanto riguarda il numeratore si ha:
$$ \Delta=16-4=12 \Rightarrow \sqrt{\Delta}=2\sqrt{3} $$
$$ x_{1,2}=\displaystyle\frac{-4\pm 2\sqrt{3}}{2} \Rightarrow \; x_1=-2-\sqrt{3}\;\;\;x_2=-2+\sqrt{3}$$
Poiché il segno della frazione e del discriminante sono discordi, la disequazione risulta verificata per valori interni all’intervallo di estremi \(x_1=(-2-\sqrt{3})\) e \(x_2=(-2+\sqrt{3})\), ovvero: \(-2-\sqrt{3}<x<-2+\sqrt{3}\).
Per quanto riguarda il denominatore, essendo un quadrato, assume sempre valori positivi.
Occorre verificare le condizioni di esistenza della frazione, per cui denominatore deve essere non nullo: \((x+1)^2 \ne0\) \(\Rightarrow\) \(\;x\ne-1\).
Dal punto di vista grafico si ha:
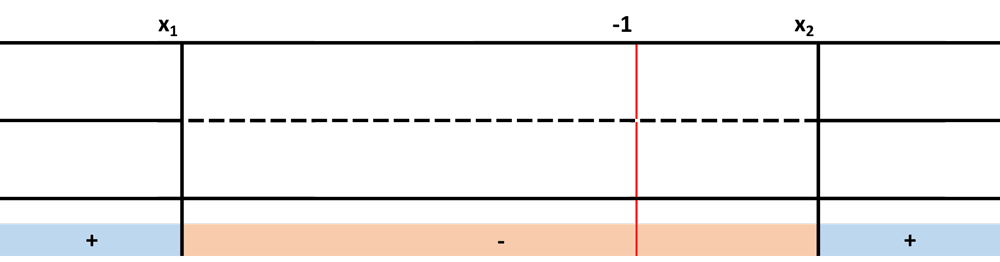
La disequazione è quindi verificata per:
$$-2-\sqrt{3}<x<-2+\sqrt{3} \;\;\;\;\;\;x\ne-1$$
Visite: 53196
